Физика
Тема 7: Электростатика и электродинамикаУрок 3: Взаимодействие нескольких зарядов
- Теория
Взаимодействие нескольких зарядов
Напряженность системы зарядов вычисляется с помощью принципа суперпозиции.
Принцип суперпозиции
Напряженность электрического поля, создаваемая системой зарядов, равна векторной сумме напряженностей, создаваемых каждым зарядом по отдельности:
E⃗ = E⃗1 + E⃗2 + E⃗3+...
Например, в случае двух зарядов, первый заряд создает в некоторой точке напряженность E⃗1 , второй – напряженность E⃗2 . Полная напряженность есть векторная сумма E⃗1 и E⃗2 :
E⃗ = E⃗1 + E⃗2
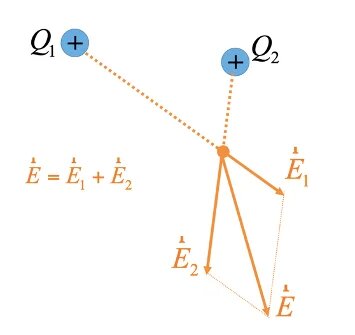
Для решения задач придерживайтесь алгоритма:
a) Запишите принцип суперпозиции в векторном виде
b) Рассмотрите принцип суперпозиции в проекции на оси координат
Задача 1
Три заряда лежащие на одной прямой: два положительных Q1 и Q2, а также отрицательный -Q3. Расстояние между соседними зарядами 2a. Какова напряженность поля в точке O посередине между зарядами Q1 и Q2?
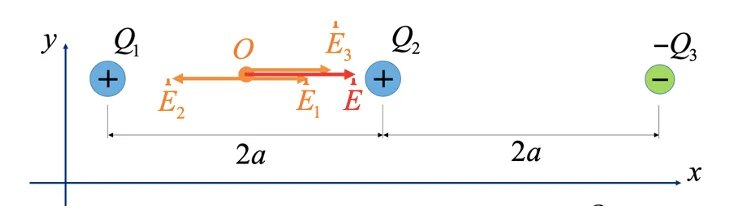
Анализ и решение:
Третий заряд равен -Q3, а его модуль |-Q3|=Q3.
Напряженности, создаваемые зарядами по отдельности:
Принцип суперпозиции в векторной форме
E⃗ = E⃗1 + E⃗2 + E⃗3+...
Создаваемая напряженность -Q3 направлена к этому заряду.
Все напряженности направлены вдоль оси x. Все проекции на ось y равны нулю.А принцип суперпозиции в проекции на ось x принимает вид:
Ex = E1 - E2 + E3
Напряженность в точке O направлена вдоль оси x, а ее проекция на эту ось равна:
Модуль напряженности равен модулю Ex : |E⃗ | = |Ex|
Задача 2
В вершинах 1 и 2 равнобедренного треугольника расположены два равных заряда Q. Какая сила будет действовать на заряд q, расположенный в 3й вершине? Длина боковой стороны b , а угол между ними 2α.
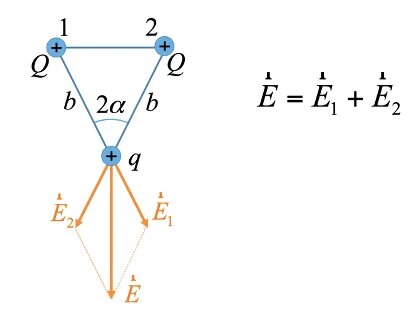
Анализ и решение
E⃗ = E⃗1 + E⃗2
В проекции на оси принцип суперпозиции принимает вид:
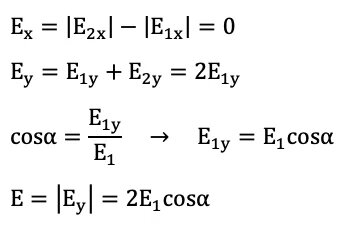
Напряженности, создаваемые каждым из зарядов:
E1=E2 =
Получаем выражение для напряженности и силы:
E=
F = qE =
Другой способ решения – с помощью закона Кулона
Fx = 0