Физика

Как запомнить формулы? Как не ошибиться? Постарайтесь разобраться в концепции. Спросите себя, какие величины в принципе должны входить в эту формулу?

Для проверки и написания формулы используйте понятие размерности: Чтобы определить длину чего-то, необходимо сравнить ее с некоторой эталонной длинной. Если "веревка имеет длину 5 метров", то имеется в виду, что ее длина в 5 раз больше эталонного объекта длиной 1 метр. Так же с любой другой величиной.

Некоторые единицы: Расстояние [м] Время [с] Масса [кг]

Операции с единицами измерения

Над размерностями можно проводить некоторые арифметические операции: их можно умножать и делить. Складывать и вычитать можно только величины одинаковых размерностей. (рис. 3.1)

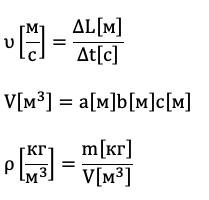
Безразмерные величины, например, отношение двух сторон треугольника. Брать функции вроде синуса, косинуса или экспоненты можно только от безразмерных величин. Так можно: sin(k[1])=ok Так нельзя: sin(V[м^3 ])≠ok

Размерности величин образуют системы. Одной из наиболее распространенных является система единиц СИ. В этой системе базовыми единицами измерения являются метр, килограмм и секунда, а также ампер, кельвин, моль, канделла. Все остальные величины могут быть из них получены, а потому называются производными. ■(Расстояние[м]@Время[с]@Масса[кг]@Ампер[А]@Кельвин[К]@Моль[моль]@Кандела[кд])  производные величины

Проверка формул Физика принципиально имеет дело с размерными величинами. И это накладывает существенные ограничения на структуру всех формул. Старайтесь проверять полученные вами формулы на размерности. Это позволит избежать ошибок.

Такая формула не верна, т.к. в ней складываются величины разных размерностей

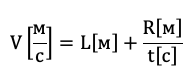
А эта формула может быть правильной

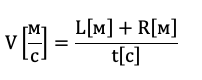
Не всегда обязательно выписывать все единицы измерения. Например, такая формула, очевидно, подходит по размерности, так как m и m_0 имеют одинаковую размерность, а выделенное синим отношение безразмерно. Например, пусть m и m_0 – некоторые массы, т.е. измеряются в кг, а R – некоторые расстояния, т.е. измеряются в метрах. Тогда в синем выражении метры сокращаются. Такая формула подходит по размерности :

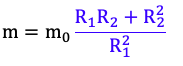
А эти формулы неверные :

 

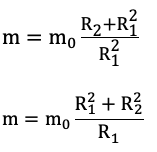
Получение формул

Для написания формулы спросите себя: какие величины в принципе должны входить в нее? Затем попробуйте составить формулу из интуитивных соображений. Воспользуйтесь размерным анализом. Например, надо получить формулу для длины окружности. На помощь приходят соображения размерности:

1) Длина окружности должна быть пропорциональна радиусу: l= r

2) Площадь окружности должна быть пропорциональна радиусу в квадрате: ■(l= r@S= r² )

3) Плюс, числовой коэффициент Pi

 

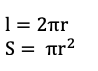
Представим, что Вам на ЕГЭ попалась вот такая задача: Сепулятор модели ЗЛ-25 с длиной канала L=1м, вокатостью

 

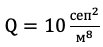
и скоростью сепуляции V=23 м/с обеспечивает поток сепуляции

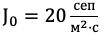
Какой будет обеспечен поток сепуляции J_1, если длина канала увеличится втрое, вокатость – в 4 раза, а скорость сепуляции V останется неизменной?

Решение: Может помочь метод размерностей. Нам известны 3 размерные величины; одну надо найти

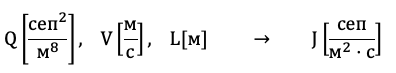
Начинаем подбирать

 

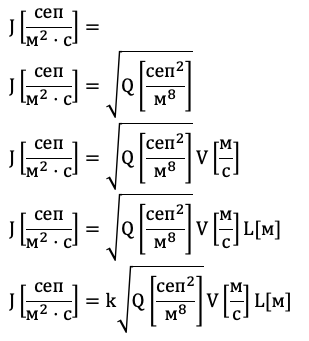
Таким образом, получаем формулу

 

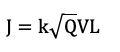
Размерный анализ – мощный инструмент, который позволяет многое, но не все. Он не заменит понимания концепции, но может дополнить его.