Информатика

Модель — образ объекта, отражающий его существенные свойства и заменяющий объект при принятии решений. У одного объекта может быть много разных моделей. 

Например, карта — это модель местности. Она отражает свойства этой местности — расположение объектов, расстояния между ними. Мы используем карету для принятия решений — как дойти от точки A к точке B.  

Модели бывают образные, знаковые и смешанные. 

Образные:

• рисунки;
• чертежи.

Смешанные:

• таблицы;
• графики;
• диаграммы;
• схемы (карты, графы, блок-схемы).

Знаковые:

• словесные описания;
• формулы.

 

Если объекты некоторой системы изобразить вершинами, а связи между ними — линиями (рёбрами), то мы получим граф.

 

 

Граф называется взвешенным, если его вершины или рёбра характеризуются дополнительной информацией — весами вершин или рёбер. На рисунке с помощью взвешенного графа изображены дороги между пятью населёнными пунктами А, В, С, D, Е; веса рёбер — протяжённость дорог в километрах.
 

>

 

Последовательность вершин, соединённых рёбрами, называется путём. Если от каждой вершины к любой другой вершине можно проложить путь, то граф обладает связностью и называется связным графом. 

 

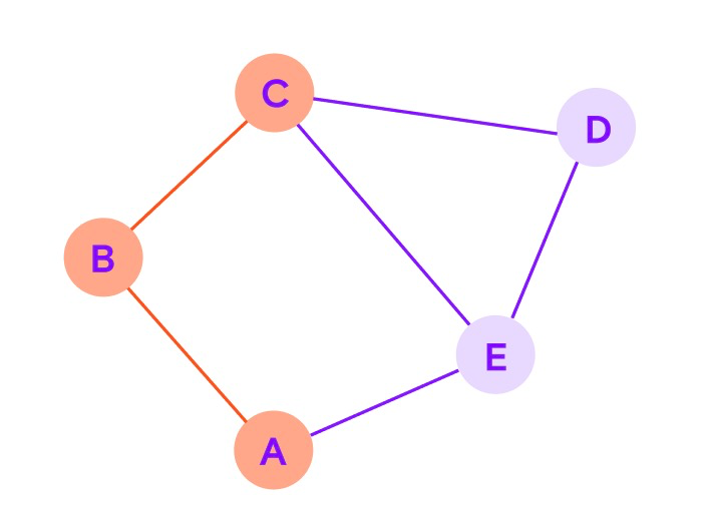
Граф с несколькими несвязанными вершинами и ребрами называется несвязным графом.

 

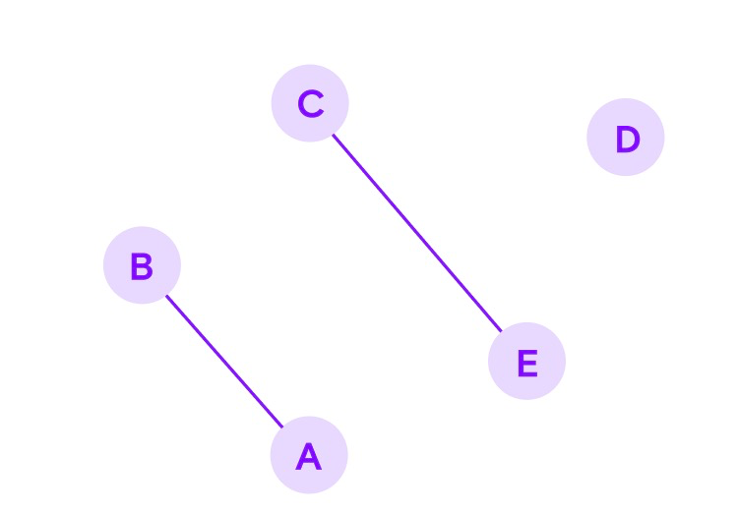
Граф может быть ориентированным, в таком случае его ребрам присвоено направление. Направление изображается стрелочками к вершинам.

 

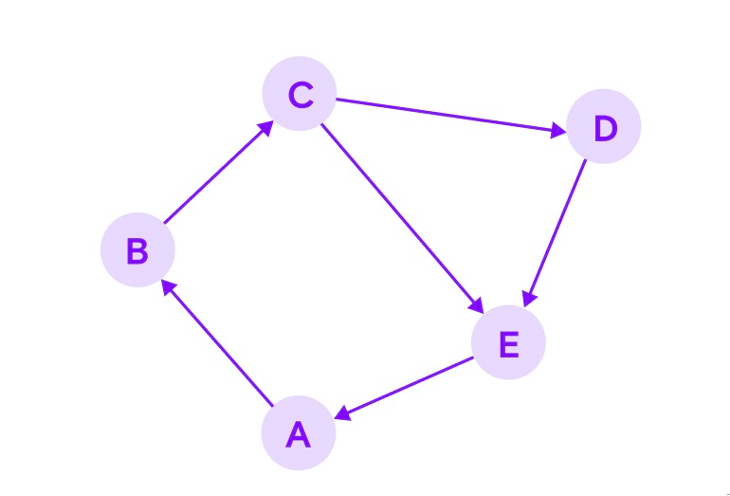
В жизни часто встречаются задачи, где нужны графы. Например, рассчитать оптимальный алгоритм для курьера, чтобы посетить все точки маршрута за минимальное время. 

В городах для планирования движения машин применяются графы совместно с искусственным интеллектом. Благодаря графам известно расстояние между перекрестками, а благодаря ИИ и распознаванию изображений видна реальная загруженность дорог — это даёт возможность управлять светофорами в онлайн режиме.

Необходимость решения задач, связанных с поиском кратчайшего пути на графе, возникает при проектировании инженерных сетей и линий электропередач, в микроэлектронике и не только.

Решение класса задач, связанного с нахождением кратчайшего пути в ориентированном графе, может состоять из следующих трёх шагов.

1) от исходного графа перейти к матрице смежности; 

Матрица смежности — это вид представления графа в виде матрицы, или двумерного массива. Каждая строка и столбец матрицы соответствуют вершинам, номер строки соответствует вершине, из которой выходит дуга, а номер столбца — в какую входит дуга.

 

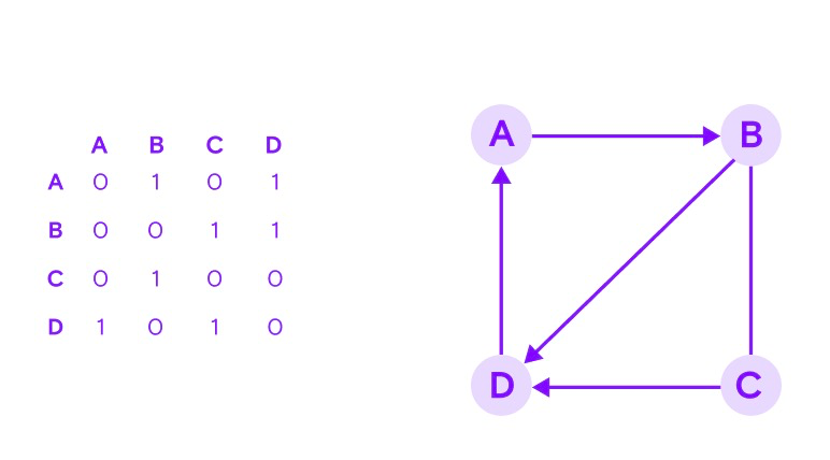
2) по матрице смежности построить дерево решений; 

Дерево решений — это особый тип графа, где вершины представлены как листья, а рёбра — как ветки. В ориентированном графе есть корень — от него исходят все ветки и листья.

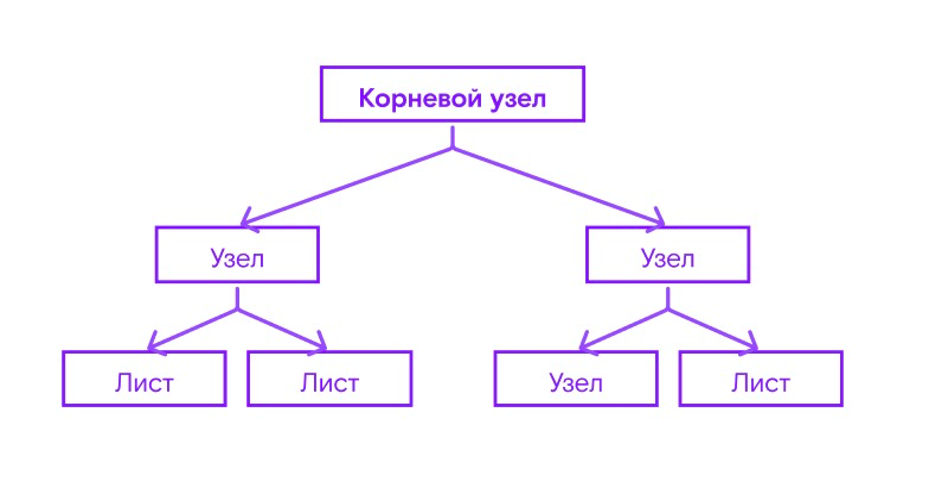
3) по дереву решений выбрать подходящий вариант.

 

В виде графа можно изобразить игру. Она характеризуется следующими признаками:

• несколько игроков;
• варианты действий → неопределенность поведения;
• наличие (несовпадение) инетересов игроков;
• взаимосвязанность поведения игроков;
• наличие правил поведения, известных всем игрокам.

Игра может быть представлена в виде дерева, каждая вершина которого соответствует ситуации выбора игроком своей стратегии. В играх с полной информацией участники знают все ходы, сделанные до текущего момента, равно как и возможные стратегии противников, что позволяет им в некоторой степени предсказать последующее развитие игры.

Выигрышная стратегия — это правило, следуя которому игрок выигрывает независимо от того, как играет противник.

 

Графы часто используются в машинном обучении, анализе данных и статистике. Графам даже посвящён специальный раздел математики — теория графов. 

Дополнительные материалы:

§1.1 Моделирование как метод познания (Информатика: учебник для 9 класса / Л.Л. Босова, А.Ю. Босова. — М.: БИНОМ. Лаборатория знаний, 2013)

§1.3 Графические информационные модели (Информатика: учебник для 9 класса / Л.Л. Босова, А.Ю. Босова. — М.: БИНОМ. Лаборатория знаний, 2013)

Глава 3. Информационное моделирование (Информатика. 11 класс. Базовый уровень / Л. Л. Босова, А. Ю. Босова. — М. : БИНОМ. Лаборатория знаний, 2016)