Информатика

Теория игр — это математический метод изучения оптимальных стратегий в играх. Под игрой понимается процесс, в котором участвуют две и более стороны, ведущие борьбу за реализацию своих интересов. 

Каждая из сторон имеет свою цель и использует некоторую стратегию, которая может вести к выигрышу или проигрышу — в зависимости от поведения других игроков. 

Теория игр помогает выбрать лучшие стратегии с учётом представлений о других участниках, их ресурсах и их возможных поступках. Специалисты в теории игр могут объяснить поведение, его рациональность или иррациональность
 

Давайте рассмотрим интересную задачу из теории игр — дилемму заключенного.

Есть двое заключенных, и им дается выбор: молчать или донести на другого. Если оба молчат, то получают меньший срок (полгода), если оба доносят — то каждый по 2 года, а вот если один донесет, а другой промолчит, то первого освободят, а второй получит 10 лет.

 

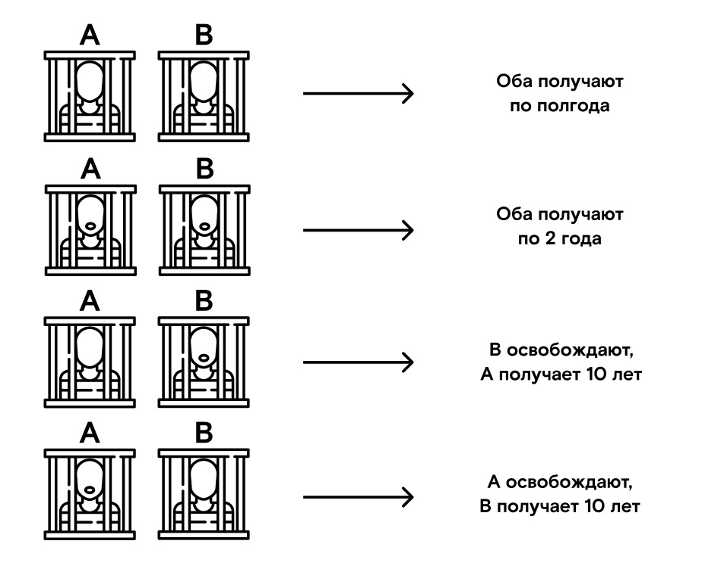
Ведя себя по отдельности рационально, вместе участники приходят к нерациональному решению: если оба предадут, они получат в сумме меньший выигрыш, чем если бы сотрудничали (молчали). Поскольку в любой ситуации предать выгоднее, чем сотрудничать, все рациональные игроки выберут предательство.

 

 

Рассмотрим следующую задачу — Петя, Ваня и камни. Петя и Ваня играют в игру, перед ними лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. 

Доступные Пете и Ване действия:

• добавить в кучу один камень (+1);
• добавить в кучу два камня (+2);
• увеличить количество камней в куче в 3 раза (×3).

Например, имея кучу из 5 камней, за один ход можно получить кучу из 6, 7 или 15 камней.

Цель игры:

• Количество камней в куче должно стать > 45.

Решение:

Для решения таких задач помогает линия чисел. Для этого выпишите возможные количества камней и отметьте выигрышные позиции.

Будем считать, что в начале игры в куче S камней, где 1 ≤ S ≤ 45.

• Если S = 45, то выигрышным будет любое действие Пети.
• Если S = 44. то выигрышным будет действие 2 и 3.
• Если S = 43, то выигрышным будет действие 3.

 

То есть при S = ≥ 16 Петя может выиграть с первого хода.

Выиграть со второго хода Петя может, если получит S = 15 после 1-го хода (тогда Ваня не сможет получить больше 45 в свой ход). 

Получить S = 15 можно при S = 14 (+1), S = 13 (+2) и S = 5 (×3).

 

Игра начинается всякий раз, когда субъекты пытаются взаимодействовать друг с другом. Поэтому теорию игр используют психологи, социологи, политики, маркетологи и многие другие специалисты.

В социологии теория игр помогает понять, объяснить и контролировать игры с социальной составляющей. Социологи пытаются понять причины действий групп игроков, для чего моделируют игры и проводят исследования, находя самые выгодные стратегии.

В психологии теория игр изучает действия каждого отдельного обособленного игрока. 

В политике теория игр применяется для анализа ситуаций и взаимодействий игроков (как правило стран), для решения игр и для поиска наилучших стратегий. У стран есть ряд конфликтов: территории, торговля, альянсы… Теория игр помогает достичь компромисса. Также теория игр применяется в голосованиях – кандидаты прибегают к разным стратегиям для увеличения шансов выигрыша.

В экономике теория игр применяется повсеместно. Экономические игры — аукционы, модели монополии и олигополии, рынки и многое другое.

Мы применяем теорию игр, даже не догадываясь об этом — когда выстраиваем логические цепочки, анализируем ситуации и придумываем стратегии.

Теория игр показывает, что не всегда наша интуиция верна. Теория может научить нас мыслить логически и проверять даже самые очевидные ситуации. А ещё теория игр может научить мыслить в более долгосрочной перспективе и учитывать большее количество деталей.